[확통]조건부확률(Coditional Probabaility)

Matching problem

j번째에 j번 카드가 있을 확률

• $$P(A_1 ∩ A_2 ∩ … ∩A_k) = \frac{(n-k)!}{n!}$$ : 1~n까지 각각의 번호에 카드를 정렬하는 경우의 수
  • 위의 항이 과연 몇 개가 존재할까? n에서 k개 만큼의 집합의 수만큼 존재
    • $${n \choose k} = \frac{n!}{(n-k)!n!}$$
• $$\frac{(n-k)!}{n!} * \frac{n!}{(n-k)!n!} …$$
• $$P(∪A_j) = 1 - \frac{1}{2!} + \frac{1}{3!} - …$$
  • 1부터 n장의 카드가 전부 자기 자리에 있을 확률
• $$P(no match) = P(∩ A_j^c) = 1 - (1 + \frac{1}{2!} - \frac{1}{3!} + …) = \frac{1}{e}$$
  • 전부 짝이 맞지 않을 확률
  • 1 - (전부 자기 자리에 있을 확률) / 합집합의 여집합 = 여집합의 교집합
• n이 무한대로 간다고 하면 확률은 어떻게 될까? 문제의 정답을 보면 답이 $$\frac{1}{e}$$ 임을 알 수 있지만 계산하기 전 보통 사람들의 대답은 e에 자리에 무한대나 엄청나게 큰 수를 부르곤 한다. 즉, j가 j번째에 있을 확률이 굉장히 드물게 일어난다고 생각하는 것이다.
• 드물게 일어나는 이 사건과 많은 시행이 경쟁하다 보면 → 결국 $$\frac{1}{e}$$로 수렴함을 알 수 있다.

Independence 독립

• 표본 공간이 있고, 다룰 확률 P가 있다고 했을 때 다음과 같은 식을 만족하면 독립이다.
• P(A ∩ B) = P(A)P(B)
• Note: Disjointness(배반) ; A가 일어났다면 B는 절대 일어날 수 없다.
  • 독립과는 전혀 다른 정의임
• A, B, C가 독립이다 IF . P(A,B) = P(A)P(B), P(A,C) = P(A)P(C), P(B,C) = P(B)P(C)만 필요할까?
  • 편의를 위해 교집합의 기호를 , 로 표현하였다.
• 답은 아님. P(A,B,C) = P(A)P(B)P(C) 도 필요
• 쌍으로도 독립이어야 하고, 셋이어도 독립이어야 하고, 몇 개를 뽑더라도 독립이어야 함

Newton Pepys Problem(1693)

다음 사건 중 어떤 사건이 가장 확률이 높을까?

A: 6개의 주사위 중 적어도 1개가 6일 확률

B: 12개의 주사위 중 적어도 2개가 6일 확률

C:18개의 주사위 중 적어도 3개가 6일 확률

• 각 주사위는 서로 독립적임
• 적어도 하나 = 합사건을 생각 →여사건 생각
• P(A) = 1 - (6개의 주사위가 모두 6이 아닐 확률) = $$1 - (\frac{5}{6})^6 = 0.655$$
• P(B) = 1 - (정부 6이 아닐 확률) - (정확히 하나는 6이고 나머지는 6이 아님) = 

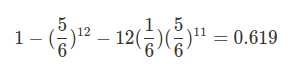
• P(C) = $$1 - \sum_{k=0}^{2}{18 \choose k}(\frac{1}{6})^k(\frac{5}{6})^(18-k) = 0.597$$

Conditional Probabilities 조건부확률

How should you update your belief/uncertainty based on new evidence?

$P(A|B) = \frac{P(A∩B)}{P(B)}, if P(B) > 0$

처음에 A가 일어날 확률만 알았음(B가 일어나리라고 확신하지는 못하는 상태)

그 다음에 B가 일어남

이 때, A와 B가 독립이 아니라면, A가 일어날 확률을 어떻게 갱신할 것인가

• 직관 1: 조약돌 세계
  • $B^C$ (B가 일어나지 않는 조약돌은 제거)
  • Renormalize : 총 질량이 1이 되도록 B로 나눠주기
    • $P(A|B) = \frac{P(A \cap B)}{P(B)}$
    • 위의 식에서 A를 B로 바꾼다고 생각했을때 P(B)로 나눠줌으로써 1이 됨
• 직관 2: 빈도학파 세계
  • 무한번 시행 (repeat infinitely)
  • 동전을 던진다고 했을때 A면과 B면이 나오는 결과를 리스트로 만든다고 가정 → 이를 무한번 시행
  • 10111000, 10111111, 11111111 ….
  • 1이 나왔던 경우만 동그라미를 치자.
  • 조건부확률은 이 동그라미 친 경우에서 A도 나온 횟수도 동그라미 친 것

이 2가지 직관적인 설명으로 조건부 확률을 이해했다면 이를 활용해 다양한 theorem들을 증명해보자.

Theorem 1

$P(A \cap B) = P(B)P(A|B) = P(A)P(B|A)$

• 위의 조건부 확률식에서 분모에 있던 P(B)를 단지 각항에 곱해준 것 뿐이다.
• P(A)P(B|A) : $P(A \cap B)$ 는 $P(B \cap A)$ 와 같기 때문에 A, B 각각의 위치를 바꿔도 성립한다.

Theorem 2

$P(A_1, …, A_n) = P(A_1)P(A_2|A_1)P(A_3|A_1, A_2) … P(A_n|A_1, … A_{n-1})$

• Factorial 정리
• Theorem 1을 n개의 A로 확장한 것이다.

Theorem 3

$P(A|B) = \frac{P(B|A)P(A)}{P(B)}$

• 베이즈 정리(Bayes’ theorem)
• Theorem 1에서 $P(B)P(A|B) = P(A)P(B|A)$ 를 $P(B)$ 로 나눠주면 위의 식이 성립한다.